[자료구조] 트리
1. 정의
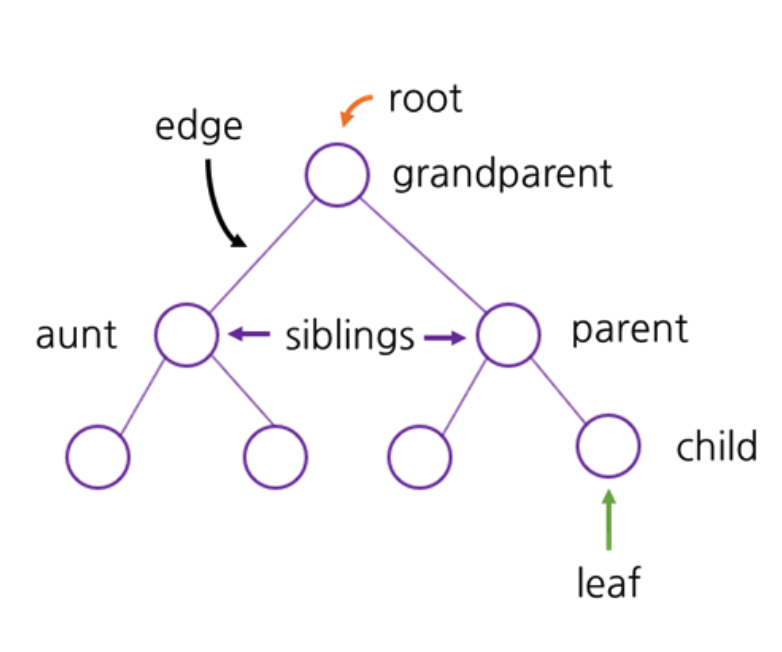
- 트리는 각각의 노드들을 간선(edge)로 연결한 자료구조로써, 각각의 노드들은 부모-자식 관계를 가진다.
- 뿌리(root): 트리의 시작
- 잎(leaf): 자식이 없는 노드
- 간선의 수에 따라 level을 나눈다.
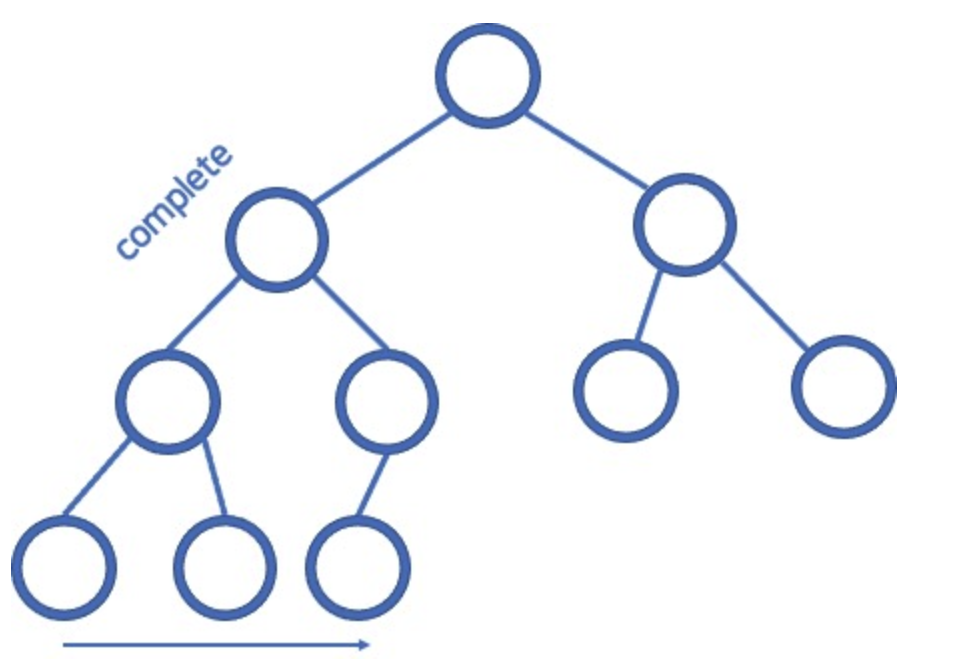
1.1 완전 트리(Complete Tree)
- 잎이 아닌 모든 노드가 2개의 자식 노드를 가지고 있고, 마지막 줄은 왼쪽에서 오른쪽 순서로 채워져 있는 트리
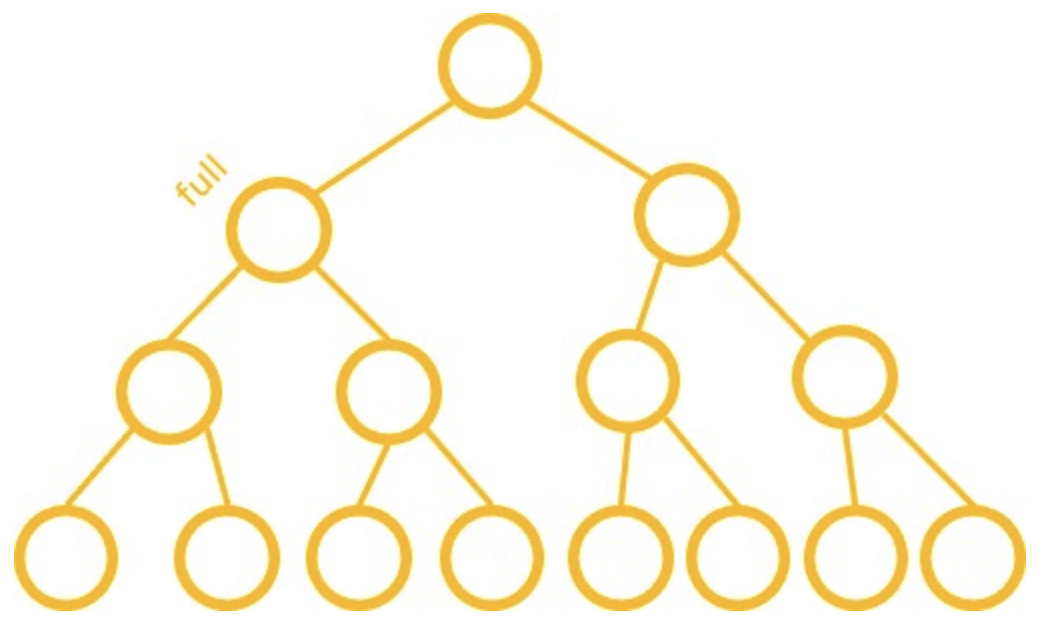
1.2 정 트리(Full tree)
- 잎이 아닌 모든 노드가 2개의 자식 노드를 가지고 있고, 모든 잎이 같은 레벨에 있는 트리
2. 순회
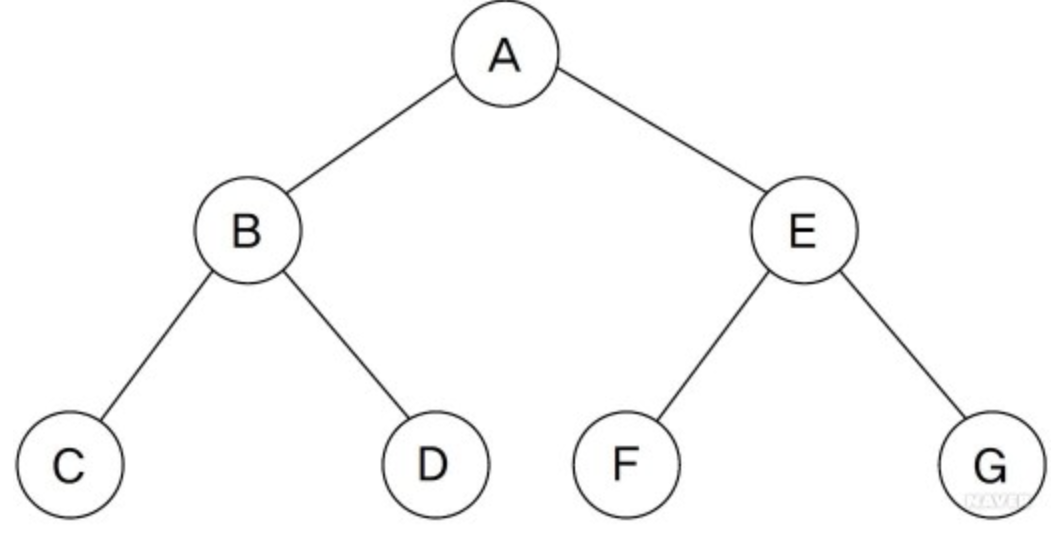
- 전위 순회(Pre order traversal / Depth first traversal) : 루트 노드에서 시작하여, 왼쪽 자식 노드로 갔다가 오른쪽 자식 노드로 가는 순회 방법
- A → B → C → D → E → F → G
- 중위 순회(In order traversal) : 왼쪽 자식 노드에서 시작하여, 루트 노드로 갔다가 오른쪽 자식 노드로 가는 순회 방법
- C → B → D → A → F → E → G
- 후위 순회(Post order traversal) : 왼쪽 자식 노드에서 시작하여, 오른쪽 자식 노드로 갔다가 루트 노드로 가는 순회 방법
- C → D → B → F → G → E → A
- 너비 우선 순회(Breadth first traversal) : 가장 위에 있는 노드에서 시작하여, 같은 레벨을 왼쪽에서 오른쪽으로 모두 탐색한 후 레벨을 높여가며 순회 하는 방법
- A → B → E → C → D → F → G
3. 구현
//트리의 노드
class Node<E> {
E data;
Node<E> left; //왼쪽 자식노드
Node<E> right; //오른쪽 자식노드
public Node(E obj) {
this.data = data;
left = null;
right = null;
}
}//추가 메서드
public void add(E obj) {
if (root == null) {
root = new Node<E>(obj);
} else {
add(obj, root)
}
currentSize++;
}
private void add(E obj, Node<E> node) { //오버 로딩
if (((Comparable<E> obj).compareTo(node.data)) > 0) { //현재 노드의 데이터보다 추가하려는 데이터가 큰 경우 오른쪽 자식으로 가야 함
if (node.right == null) { //자식이 없다면
node.right = new Node<E>(obj);
return;
}
return add(obj, node.right); //자식이 있으면 한 번 더 비교
}
if (node.left == null) { //자식이 없다면
node.left = new Node<E>(obj);
return;
}
return add(obj.node.left); // 자식이 있으면 한 번 더 비교
}
//contains 메소드
public boolean contains(E obj) {
return contains(obj, root);
}
private boolean contains(E obj, Node<E> node) {
if (node == null) { //노드가 없으면
return false;
}
if (((Comparable<E>) obj).compareTo(node.data) == 0) { //노드와 데이터가 같으면
return true;
}
if (((Comparable<E>) obj).compareTo(node.data) > 0) { //노드가 데이터 보다 크면
return contains(obj, node.right);
}
return contains(obj, node.left); //나머지
}
- 삭제 메서드 원리
- leaf 노드 제거 - leaf 노드의 부모 노드의 포인터를 null 처리
- 자식 노드가 하나인 노드를 제거 - 이 노드의 부모 노드의 포인터를 이 노드의 자식 노드로 향하게 하면 됨
- 자식 노드가 두 개인 노드를 제거 - 중위 후속자(루트보다 바로 직전인 노드)와 중위 선임자(루트 다음번째 노드) 중 하나와 자리를 바꾼 후 노드 제거
4. 회전
- 트리의 균형이 잡혀 있지 않으면 트리를 회전 시켜서 균형을 잡아야 한다.
- 트리가 한 쪽으로 치우친 경우
- 불균형이 왼쪽 서브트리에서 나타날 경우
- 조부모 노드를 오른쪽으로 회전 시켜야 한다
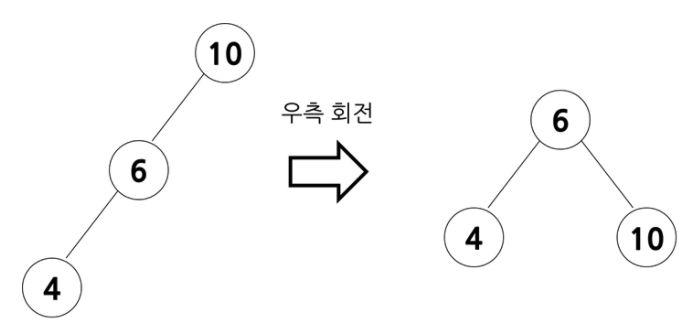
- 불균형이 오른쪽 서브트리에서 나타날 경우
- 조부모 노드를 왼쪽으로 회전 시켜야 한다.

- 불균형이 왼쪽 서브트리에서 나타날 경우
- 트리가 치우치지 않은 경우
- 불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
- 부모 노드를 오른쪽으로 회전 시킨 후 조부모 노드를 왼쪽으로 회전시켜야 한다.

- 불균형이 왼쪽 자식의 오른쪽 서브 트리에서 나타날 경우
- 부모 노드를 왼쪽으로 회전 시킨 후 조부모 노드를 오른쪽으로 회전시켜야 한다.

- 불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
-
//좌측 회전: 조부모 노드를 부모 노드의 왼쪽 자식 노드로 옮김 public Node<E> leftRotate(Node<E> node) { Node<E> tmp = node.right; node.right = tmp.left; tmp.left = node; return tmp; } //우측 회전: 조부모 노드를 부모 노드의 오른쪽 자식 노드로 옮김 public Node<E> rightRotate(Node<E> node){ Node<E> tmp = node.left; node.left = tmp.right; tmp.right = node; return tmp; }
※ 참조
'CS > [DATA STRUCTURE]' 카테고리의 다른 글
| [자료구조] AVL트리 (0) | 2022.03.08 |
|---|---|
| [자료구조] 힙 (0) | 2022.03.03 |
| [자료구조] 해시 (0) | 2022.02.24 |
| [자료구조] 연결 리스트(Linked List) (0) | 2022.02.22 |
| [자료구조] 스택과 큐 (0) | 2022.02.17 |
[자료구조] 트리
1. 정의

- 트리는 각각의 노드들을 간선(edge)로 연결한 자료구조로써, 각각의 노드들은 부모-자식 관계를 가진다.
- 뿌리(root): 트리의 시작
- 잎(leaf): 자식이 없는 노드
- 간선의 수에 따라 level을 나눈다.
1.1 완전 트리(Complete Tree)
- 잎이 아닌 모든 노드가 2개의 자식 노드를 가지고 있고, 마지막 줄은 왼쪽에서 오른쪽 순서로 채워져 있는 트리

1.2 정 트리(Full tree)
- 잎이 아닌 모든 노드가 2개의 자식 노드를 가지고 있고, 모든 잎이 같은 레벨에 있는 트리

2. 순회

- 전위 순회(Pre order traversal / Depth first traversal) : 루트 노드에서 시작하여, 왼쪽 자식 노드로 갔다가 오른쪽 자식 노드로 가는 순회 방법
- A → B → C → D → E → F → G
- 중위 순회(In order traversal) : 왼쪽 자식 노드에서 시작하여, 루트 노드로 갔다가 오른쪽 자식 노드로 가는 순회 방법
- C → B → D → A → F → E → G
- 후위 순회(Post order traversal) : 왼쪽 자식 노드에서 시작하여, 오른쪽 자식 노드로 갔다가 루트 노드로 가는 순회 방법
- C → D → B → F → G → E → A
- 너비 우선 순회(Breadth first traversal) : 가장 위에 있는 노드에서 시작하여, 같은 레벨을 왼쪽에서 오른쪽으로 모두 탐색한 후 레벨을 높여가며 순회 하는 방법
- A → B → E → C → D → F → G
3. 구현
//트리의 노드
class Node<E> {
E data;
Node<E> left; //왼쪽 자식노드
Node<E> right; //오른쪽 자식노드
public Node(E obj) {
this.data = data;
left = null;
right = null;
}
}//추가 메서드
public void add(E obj) {
if (root == null) {
root = new Node<E>(obj);
} else {
add(obj, root)
}
currentSize++;
}
private void add(E obj, Node<E> node) { //오버 로딩
if (((Comparable<E> obj).compareTo(node.data)) > 0) { //현재 노드의 데이터보다 추가하려는 데이터가 큰 경우 오른쪽 자식으로 가야 함
if (node.right == null) { //자식이 없다면
node.right = new Node<E>(obj);
return;
}
return add(obj, node.right); //자식이 있으면 한 번 더 비교
}
if (node.left == null) { //자식이 없다면
node.left = new Node<E>(obj);
return;
}
return add(obj.node.left); // 자식이 있으면 한 번 더 비교
}
//contains 메소드
public boolean contains(E obj) {
return contains(obj, root);
}
private boolean contains(E obj, Node<E> node) {
if (node == null) { //노드가 없으면
return false;
}
if (((Comparable<E>) obj).compareTo(node.data) == 0) { //노드와 데이터가 같으면
return true;
}
if (((Comparable<E>) obj).compareTo(node.data) > 0) { //노드가 데이터 보다 크면
return contains(obj, node.right);
}
return contains(obj, node.left); //나머지
}
- 삭제 메서드 원리
- leaf 노드 제거 - leaf 노드의 부모 노드의 포인터를 null 처리
- 자식 노드가 하나인 노드를 제거 - 이 노드의 부모 노드의 포인터를 이 노드의 자식 노드로 향하게 하면 됨
- 자식 노드가 두 개인 노드를 제거 - 중위 후속자(루트보다 바로 직전인 노드)와 중위 선임자(루트 다음번째 노드) 중 하나와 자리를 바꾼 후 노드 제거
4. 회전
- 트리의 균형이 잡혀 있지 않으면 트리를 회전 시켜서 균형을 잡아야 한다.
- 트리가 한 쪽으로 치우친 경우
- 불균형이 왼쪽 서브트리에서 나타날 경우
- 조부모 노드를 오른쪽으로 회전 시켜야 한다

- 불균형이 오른쪽 서브트리에서 나타날 경우
- 조부모 노드를 왼쪽으로 회전 시켜야 한다.

- 불균형이 왼쪽 서브트리에서 나타날 경우
- 트리가 치우치지 않은 경우
- 불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
- 부모 노드를 오른쪽으로 회전 시킨 후 조부모 노드를 왼쪽으로 회전시켜야 한다.

- 불균형이 왼쪽 자식의 오른쪽 서브 트리에서 나타날 경우
- 부모 노드를 왼쪽으로 회전 시킨 후 조부모 노드를 오른쪽으로 회전시켜야 한다.

- 불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
-
//좌측 회전: 조부모 노드를 부모 노드의 왼쪽 자식 노드로 옮김 public Node<E> leftRotate(Node<E> node) { Node<E> tmp = node.right; node.right = tmp.left; tmp.left = node; return tmp; } //우측 회전: 조부모 노드를 부모 노드의 오른쪽 자식 노드로 옮김 public Node<E> rightRotate(Node<E> node){ Node<E> tmp = node.left; node.left = tmp.right; tmp.right = node; return tmp; }
※ 참조
'CS > [DATA STRUCTURE]' 카테고리의 다른 글
| [자료구조] AVL트리 (0) | 2022.03.08 |
|---|---|
| [자료구조] 힙 (0) | 2022.03.03 |
| [자료구조] 해시 (0) | 2022.02.24 |
| [자료구조] 연결 리스트(Linked List) (0) | 2022.02.22 |
| [자료구조] 스택과 큐 (0) | 2022.02.17 |
